U velikom broju praktičnih problema promatranje signala kao funkciju vremena ne pruža dovoljno informacija o samoj prirodi promatrane pojave, te dolazi do potrebe za uvidom u frekvencijski sadržaj signala što je moguće napraviti pomoću Fourierove transformacije. Međutim, Fourierovom transformacijom signala gube se njegove vremenske značajke, te je stoga ovakav pristup neprimjeren za nestacionarne signale, tj. signale čija se frekvencija mijenja kroz vrijeme. Pri analizi nestacionarnih signala poželjno je promatrati energiju signala kao funkciju i vremena i frekvencije istodobno, pa se takav prikaz naziva vremensko-frekvencijska distribucija (TFD) signala.
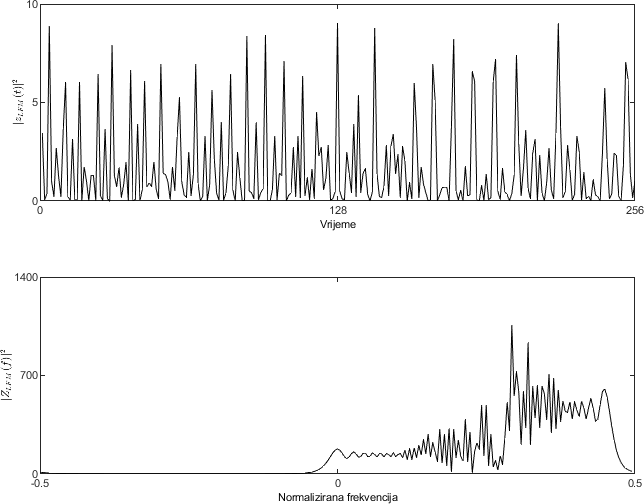
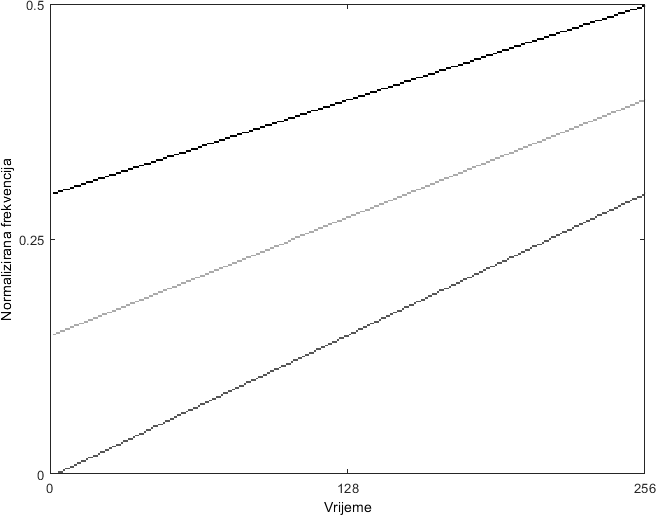
Računski najjednostavnije TFD su one linearne, prvenstveno Fourierova transformacija na vremenskom otvoru (STFT) i Gaborova transformacija. No, linearne TFD imaju ograničenu rezoluciju, te uobičajeno podrazumijevaju kompromis između rezolucije u vremenu i rezolucije u frekvenciji, stoga se u praksi najčešće koriste kvadratne TFD (QTFD).
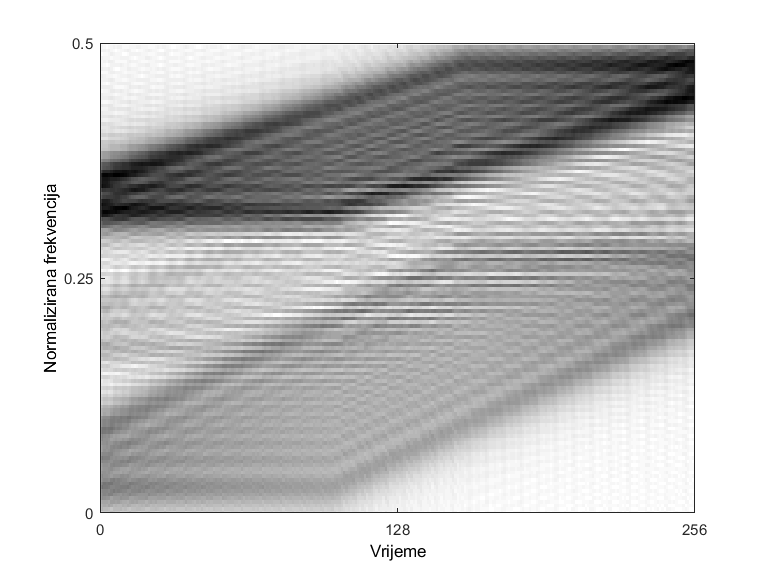
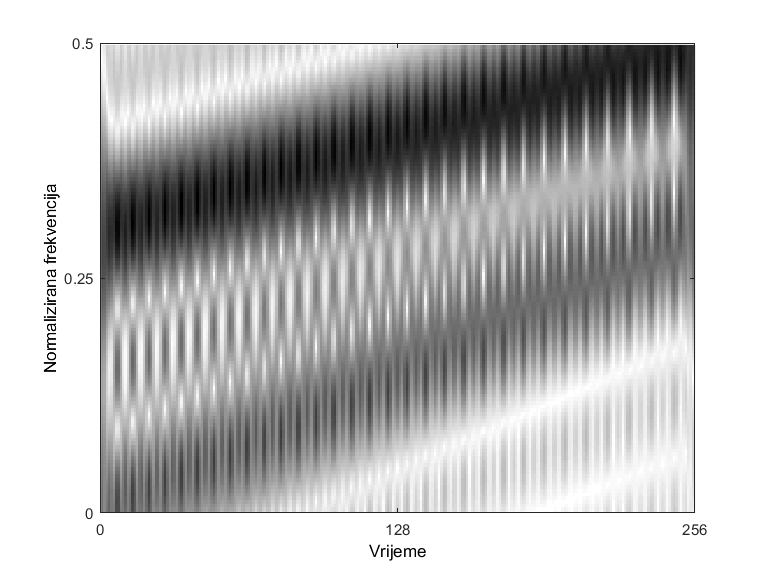
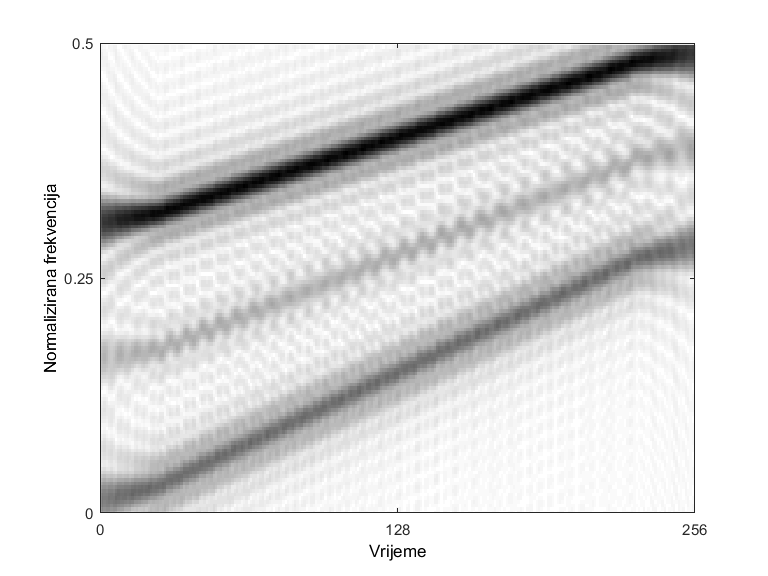
No, kada se signal sastoji od više komponenti ili sadrži komponentu s nelinearnom frekvencijskom modulacijom, zbog svoje kvadratne prirode, QTFD uvode neželjene članove, tzv. artefakte ili među-članove, koji se pojavljuju između svakog para komponenti signala te uvelike otežavaju interpretaciju QTFD. Pošto su među-članovi visoko oscilatorni, u domeni neodređenosti, tj. dvodimenzionalnoj Fourierovoj transformaciji TFD, među-članovi su locirani dalje od ishodišta domene, stoga ih je moguće filtrirati s nisko-propusnim filtrom. Međutim, filtriranje na opisani način uklanja i dio korisnih informacija, tzv. auto-članove, što dovodi do gubitka rezolucije TFD-a.
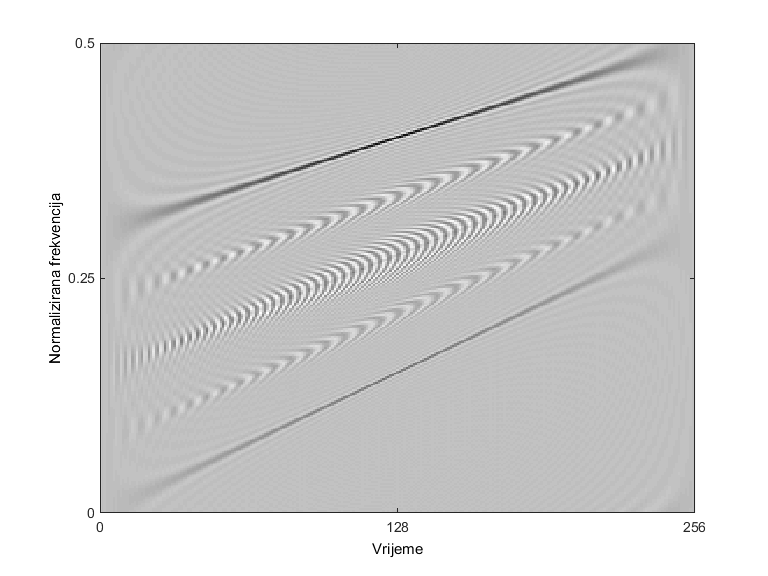

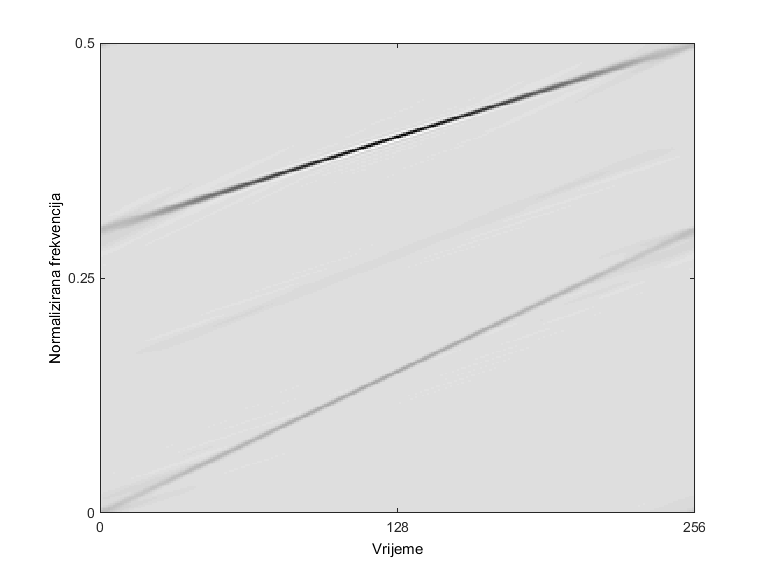
Osnovna, nefiltrirana QTFD naziva se Wigner-Villeova distribucija (WVD), a primjenom 2D nisko-propusnog filtra u domeni neodređenosti, moguće je dizajnirati beskonačan broj različitih QTFD s različitim vrstama kompromisa između učinkovitosti uklanjanja među-članova i gubitka rezolucije auto-članova. U literaturi među korištenijim QTFD-ovima nalaze se: izglađena pseudo WVD, Choi-Williams distribucija, Born-Jordan distribucija, B distribucija, te njene modifikacije. Bolje performanse QTDF-a mogu se postići nezavisnim filtriranjem po vremenu i po frekvenciji, ali takve metode često zahtijevaju a priori poznavanje prirode promatranog signala, što u praksi najčešće nije slučaj.